Mathematical Foundations of Computer Science
Introduction
The notes on Mathematical Foundations (or the Theory of Computation) presented below are mainly based on
Cohen, Daniel (1997), Introduction to Computer Theory, 2nd Edition, John Wiley & Sons,
and Hopcroft, J., Motwani, R. & Ullman, J. (2007), Introduction to Automata Theory, Languages, and Computation, 3rd Edition, Addison Wesley,
and Sipser, M. (2012) Introduction to the Theory of Computation, Cengage Learning, 3rd edition.
We will emphasize mathematical models of computation in this session.
Chapter 1 of Cohen (1997) includes a brief history of the subject; read it and pay attention to the following questions:
1. What was the main theme of David Hilbert's speech in 1900 that turned out to be of major significance to the development of computer science?
2. What was the 10th problem on Hilbert's list?
3. What did Turing prove about his abstract machine?
4. How did World War II affect the development of the computer?
The way we shall be studying about computers is to build mathematical models, which we shall call machines,
and then to study their limitations by analyzing the types of input on which they operate successfully.
(Cohen 1997, page 3).
The most important mathematical models are Finite Automata (FA), Pushdown Automata (PDA), and Turing Machines (TMs). The most
powerful automata are the Turing Machines developed by Alan Turing (1936) because these machines can process (accept) all
recursively enumerable sets (or computable languages) whereas Pushdown Automata can process a proper subset called Context-Free languages,
and Finitie Automata can process a proper subset (Regular languages) of Context-Free languages. Our main goal is to
understand the relationship among these languages and their corresponding automata
(FA, PDA and TMs) as shown in the diagram given below.

Diagram 1: Elements of the Automata Theory
Please note that RG = Regular Grammar, CFG = Context-Free Grammar, UG = Unrestricted Grammar (or Unrestricted Phrase Structure Grammar).
Turing's goal was to describe precisely the boundary between what a computing machine could do and what
it could not do; his conclusions apply not only to his abstract Turing Machines, but
to today's real machines.
(Hopcroft, Motwani & Ullman 2007, Page 1). Today's computers are Turing Machines. Pushdown Automata (PDA) are computationally less powerful than Turing Machines and Finite Automata (FA) are less powerful than PDA. One of the best ways to understand the computing power of automata is to examine the way in which various sets are processed by these automata. These sets are also called languages because these sets can be also defined by grammars following Noam Chomsky's suggestions. If you are not familiar with grammar formalisms, you can skip the grammatical aspects initially.
Overview
Automata theory provides theoretical (or mathematical) foundations to computer science. In this section we discuss
some intuitive relationship among the primary automata
classes: Finite Automata (FA), Pushdown Automata (PDA), and Turing Machines (TMs).
It is good to start with a Finite Automaton for processing a regular language (or set), because Finite Automata are easy to understand. Consider the following set or language:
{a, ab, abb, abbb, abbbb, abbbbb, . . . }
The elements of the set are separated by commas; each element is a string (or token). There is a regular expression for every regular language (or set). In other words, a regular expression denotes a set. Thus, ab* is a regular expression that denotes the above set. The * at the end of ab* is known as Kleene-star. By ab* Kleene implied one a followed by zero or more b's. We can write
ab* = {a, ab, abb, abbb, abbbb, abbbbb, . . . }.
The following finite automation accepts every string of the set denoted by ab*.
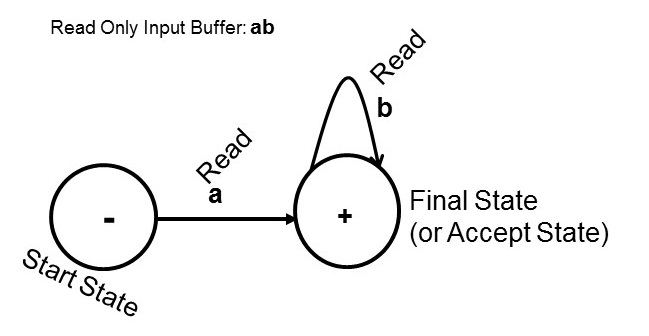
Diagram 2: A Finite Automaton for ab* (using Cohen's notation)
The above finite automaton accepts the string
a by starting at the start state (marked by -) and taking the transition (arrow) marked by
a it reaches the final state (or accept state). The same automaton accepts the string
ab because it starts from the start state, and then takes transition (arrow) marked by
a and then reaches the final state and then takes loop transition marked by
b and comes back to the final state (or accept state). The accepting conditions for FA are: (1) the input must be finished (i.e., no more symbols to scan), (2) the automaton is in a final state.
Compared to Finite Automata, Turing Machines (TMs) are more powerful because they can read, write, move the Tape-Head (Read-Write-Head) forward (Right), or backward (Left). A TM for the same set is given below:

Diagram 3: A Turing Machine for ab* (using Cohen's notation)
As shown in Diagram 3, every transition (arrow) in a TM has three components (Read, Write, Move). A TM accepts an input string by reaching the Halt state. The execution of a TM halts at the entrance to the Halt state; the Halt state cannot have a out going transition. Finite Automata (FA) cannot accept non-regular languages; Turing Machines (TMs) can accept regular and non-regular languages (that is, all recursively enumerable languages or sets). Cohen (1997) presents a proof for showing that Read only Turing Machines are equivalent to Finite Automata. In many programming languages equal number of {'s and }'s must be matched which cannot be done with Finite Automata. The following Turing Machine accepts strings such as
{}, {{}}, {{{}}}, {{{{}}}}, that characterize many programming languages;

Diagram 4: A Turing Machine for { {n }n } with a trace for {{}}
Turing Machines (TMs) are also known as algorithm machines, because every algorithm can be expressed as a TM. TMs are the most powerful well-defined machines. Finite Automata (FA) are useful for regular languages which are relatively simple sets denoted by regular expressions; they are not good for non-regular languages. Pushdown Automata (PDA) are acceptors of Context-Free Languages(CFLs) that include programming languages, because syntax of programming languages can be defined by Context-Free Grammars (CFGs). PDA can process programming languages efficiently by using a stack. There are other aspects of theoretical foundations that have great implications for scope and limitations of computer science that we will study.
Why Study Automata Theory (see Hopcroft, Motwani & Ullman 2007, page 2)
There are several reasons why the
study of automata and complexity is an important part of the core of Computer
Science. The
principal motivation and some of the important applications are briefly
mentioned below:
(1) Software for designing and checking the
behavior of digital circuits is modeled with Finite Automata (FA).
(2) Finite Automata (FA)
model and define the
lexical analyzer of a typical compiler where the input text is broken into
logical units such as identifiers, keywords, and punctuation.
(3) Software for searching large bodies of text
is also modeled in Finite Automata (FA).
(4) The
Syntax Analyzer of a typical compiler is modeled by Pushdown Automata (PDA).
(5)
Turing
Machines (TMs) define and model computability in the most elegant form.
TMs also allow clear distinction between
intractable and tractable computation. TMs define un-decidable problems in an elegant way.
(6) A
processing framework for every computable set can be given by TMs.
FINITE AUTOMATA (See Hopcroft, Motwani & Ullman (2007) Chapter 2 & 3, Cohen (1997) Chapters 4-6, and Sipser (2012)Chapter 1)
This section introduces "Regular Expressions", "Regular Languages" and Finite Automata (FA). A finite automaton is an abstract machine which can
process words or strings from a Regular Language or Regular Expressions. These terms will be defined after some intuitive introductions. An FA is a machine that reads an input string or word one character at a time from a Read Only Input Buffer.
Consider the following FA, which is a Deterministic FA:

Figure 1: A Finite Automaton (using Sipser's notation) for ab* = {a, ab, abb, abbb, abbbb, abbbbb, . . . }
Assume that abb is given as an input to this FA. Beginning in the start state, the machine reads the first letter which is a and takes the transition marked by a and goes to the state q1 . From the state q1 the machine reads the next character which is a b and takes the loop transition marked by b . The machine then reads the next character which is a b and takes the same loop transition again. By now the machine has finished the input string and ends in the final state or accept state and therefore, it accepts the input. The same FA can be represented in a different notation as in Figure 2; this notation is popularized by Cohen (1997).
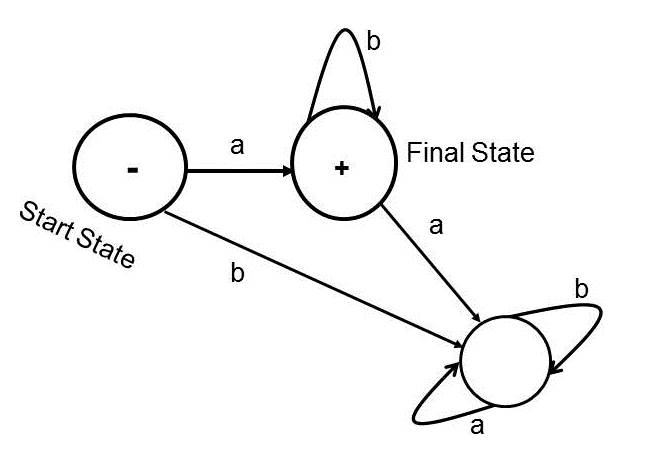
Figure 2: A Finite Automaton (FA) for ab*
in the notation of Cohen (1997)
A type of dynamic visualization of the above FA is given at:
http://www.asethome.org/fa/. For a demonstration, please click here.
For a definition of FA, please click here or visit http://www.asethome.org/fa/fa_regularExpression.html.
A non-deterministic finite Automaton (NFA) for ab* is given in Figure 3 which looks simpler than the deterministic FA (DFA) given in Figure 2. However, the DFA of Figure 2 and the NFA of Figure 3 are equivalent, because both accept every string from the set {a, ab, abb, abbb, abbbb, abbbbb, . . . } = ab*.
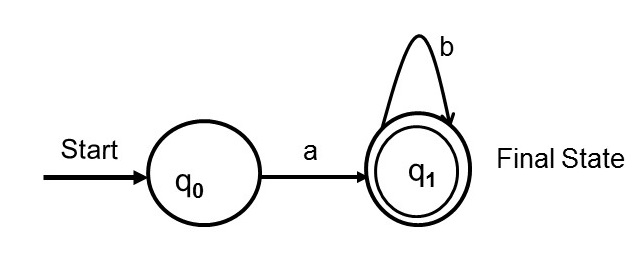
Figure 3: A Non-deterministic Finite Automaton (NFA) for ab*
The above NFA of Figure 3 is represented in Figure 4 in the notation of Cohen (1997).
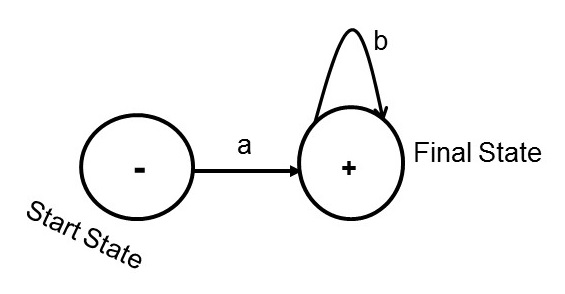
Figure 4: A Non-deterministic Finite Automaton (NFA) for ab* in the notation of Cohen (1997)
LANGUAGES
We begin our study of computation considering the nature of input, that is, the strings that may be given as input to a machine or automata. In order to study the input strings or string patterns precisely, formal languages are proposed. By formal we don't mean dressed up, we mean
languages with a form defined by rules that say which strings are in the
language and which are not. We are only interested in syntax here, not
semantics (meaning). We are interested in the form of a string of symbols, not the
meaning of the string.
The finite set of symbols that we will
use to build our strings is called the alphabet. We will have rules that
tell us how to put symbols together to form valid strings called words or
strings. The entire set of valid strings is called a language. In
other words, a language is a set of
well-formed strings.
We will find it useful to have a
string containing no symbols, the empty string or null string  .
No matter what our alphabet is, we will always use
.
No matter what our alphabet is, we will always use  �for the empty string. We will not allow
�for the empty string. We will not allow  �to be a symbol in any alphabet. Some books use epsilon for the null string or empty string.
�to be a symbol in any alphabet. Some books use epsilon for the null string or empty string.
We also have a symbol for an empty
language. Since a language is a set, the empty language is the empty set 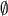 . Note that
. Note that  �is not the same as
�is not the same as  �because their data types are different.
�because their data types are different.
Note that our author substitutes + for
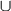 �to do the union of sets. L + {
�to do the union of sets. L + {  �} adds the empty string to the strings of
language L to form a new language.
�} adds the empty string to the strings of
language L to form a new language.
We will use the symbol Σ
as the name for alphabets the way we use L as
the name for a language.��  �is a set of symbols from which strings of the
language are made.
�is a set of symbols from which strings of the
language are made.
One way to define a language is to
list the words in that language, but if the language is infinite we certainly
can't do that. In such a case we make use of rules describing the words in the
language.
Examples
-
Σ = {a}
L1 = { ^, a, aa, aaa, aaaa, aaaaa, . . . } = a*
This language consists of the null string, a string of one a, a string of two a's, a string of three a's, and
strings of more a's. The a's
are concatenated together to build strings such as�� aa,�
aaa� and aaaa.� L1 ��includes every string that can be made
from a.��������� a3��� means
three a�s concatenated together,�
that is� aaa.
In the context of strings, superscripts denote repetition, not numerical exponentiation. That is,
a4 means aaaa. Thus, a n means n a's concatenated together.
If we need to have
variables that can be instantiated to one of the words in L1, we
will use names such as X or Y. Let X = a3 and Y = a5.
Then XY = a3a5 = a3+5 = a8 =� aaaaaaaa.�
For L1,
any two words that we concatenate together will form another word in L1.
So, we say that L1 is closed under concatenation. This is not
always true for every language.
A language similar to L1 is:
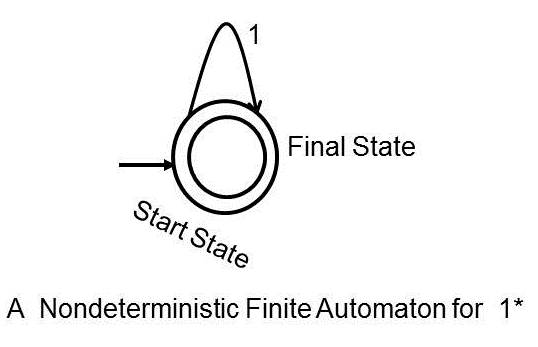
L12 = { ^, 1, 11, 111, 1111, 11111, 111111, . . . } = 1*
A machine for 1* is given below, where = { 1 }:
- L2
= {ai | i
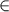
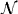 and i is odd}.
and i is odd}.
Is L2 closed under concatenation? Consider the concatenation of
a and aaa, both of which are elements of L2. Is aaaa in L2?
No! So L2 is not closed under concatenation.
L2 = { a, aaa, aaaaa, aaaaaaa, . . . }
3.  �= {a, b}
�= {a, b}
L3 =� �{ ^,
a, b, aa, ab, ba, bb,� aaa, aba, aab,
abb, baa, bba, bab, bbb, . . . }� =� (a+b)* = (a U b)*
L3 ��has all possible strings made from a and b in
any combination.� The �*� is called the
Kleene star.��
The length
of a string is the number of symbols in the string. The length of  is
0. The length of�� aab� is 3.
is
0. The length of�� aab� is 3.
 �= { a,b }
�= { a,b }
PALINDROME = { and all strings x such that x = reverse(x)}
and all strings x such that x = reverse(x)}
= { ,
a, b, aa, bb, aaa, aba, bbb, bab, ...}
,
a, b, aa, bb, aaa, aba, bbb, bab, ...}
Is PALINDROME
closed under concatenation? (no)
How about under reverse? (yes)
 �= {0,1}
�= {0,1}
Suppose we want to allow a language to contain any string made from this
alphabet including the empty string. We have some notation for that:
 *
= {0,1}* = {
*
= {0,1}* = { ,
0, 1, 00, 01, 10, 11, 000, 001, 010, 011, 100, 101, 110, 111, ...}
,
0, 1, 00, 01, 10, 11, 000, 001, 010, 011, 100, 101, 110, 111, ...}
We call the * the
Kleene star. We call the language  * the Kleene closure
or just the closure of
* the Kleene closure
or just the closure of  .
.
If  = {a,b,c} then
= {a,b,c} then  * = {
* = { ,
a,b,c,aa,ab,ac,ba,bb,bc,ca,cb,cc,...}. The order in which we list the symbols
a,b,c when we write the alphabet determines the relationship we use to put
words in "alphabetical order". When we list some of the words of a
formal language, we don't use straight alphabetical order. Instead we put them
in lexicographic order. This means that we list the words first by
length and then within a group that have the same length we use alphabetical
order.
,
a,b,c,aa,ab,ac,ba,bb,bc,ca,cb,cc,...}. The order in which we list the symbols
a,b,c when we write the alphabet determines the relationship we use to put
words in "alphabetical order". When we list some of the words of a
formal language, we don't use straight alphabetical order. Instead we put them
in lexicographic order. This means that we list the words first by
length and then within a group that have the same length we use alphabetical
order.
- We can use the
Kleene star to make strings of words just as we use it to make strings of
characters.
 = {a,b}
= {a,b}
S = {aa,b}
S* = { ,
b, aa, bb, aab, baa, bbb, aaaa, aabb, baab, bbaa, bbbb, ...}
,
b, aa, bb, aab, baa, bbb, aaaa, aabb, baab, bbaa, bbbb, ...}
 = {a,b}
= {a,b}
S = {a, ab}
S* = { ,
a, aa, ab, aaa, aab, aba, aaaa, aaab, aaba, abaa, abab, ...}
,
a, aa, ab, aaa, aab, aba, aaaa, aaab, aaba, abaa, abab, ...}
= strings over  that start with a and never
contain bb.
that start with a and never
contain bb.
To prove that a
word such as aaabaaba is in S*, we have to break it down into concatenated a's
and ab's. We call this factoring.
aaabaaba = (a)(a)(ab)(a)(ab)(a).
In this language a
word has only one possible factoring. That is not always the case. It is
certainly not the case when  contains only one symbol.
contains only one symbol.
 � = {x}
� = {x}
S = {xx, xxx}
S* = { ,
xx, xxx, xxxx, ...}
,
xx, xxx, xxxx, ...}
xxxxx = (xx)(xxx) = (xxx)(xx)
Can we make all
strings of x's with length > 1 out of xx and xxx? How? Try to describe an
algorithm with cases. That is, tell how to make any string of even length and
in a separate case how to make any string of odd length. Or mod the length of
the string by 3 and tell what to do in each of the three possible cases. These
types of algorithms are called constructive algorithms and are often
used to prove that some particular thing can always be done. Telling how to do
it for all possible cases proves that it can always be done.
There are only two cases in which a
Kleene closure is not an infinite set. If  =
= 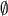 , then
, then  * = {
* = { }.
And if S = {
}.
And if S = { }
then S* = {
}
then S* = { }
because
}
because 
 =
=
 .
.
We have another operator, the
superscripted +, which means "1 or more of". Forming  + is very much like
+ is very much like  * but we omit
* but we omit  .
We call this operator the positive closure operator.
.
We call this operator the positive closure operator.
Can we take the closure of an infinite
set? What is ( *)*?
*)*?
 = {a,b}
= {a,b}
 * = {
* = { ,
a, b, aa, ab, ba, bb, ...}
,
a, b, aa, ab, ba, bb, ...}
( *)* = {
*)* = { ,
a, b, aa, ab, ba, bb, ...}
,
a, b, aa, ab, ba, bb, ...}
Theorem 1.
For any set S of strings, S* = S**.
Proof. The proof of this theorem involves double factoring. Strings in
S** are concatenations of strings in S*, which are concatenations of strings in
S. So any string in S** can be factored into strings in S.
A more formal proof is in the
textbook. To prove that two sets are equal we divide the proof into two parts.
To show A = B we show that A 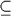 B and B
B and B 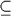 A and. Note that our author uses
A and. Note that our author uses 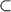 the way we use
the way we use 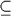 .
.
Defining a set
recursively is a 3-step process. Here is an example in which we define the set
of positive even numbers.
- Basis:
2 is in the set EVEN.
- Inductive
step: If x is in EVEN then so is� x + 2.
- Closure:
Nothing else is in EVEN.
In the basis step we place one or more
elements into the set to give ourselves a starting point. In the inductive step
we describe rules that tell how to take elements that are already in the set
and make new elements to put in the set. The closure step is always the same so
we can omit it as long as everybody understands that it is still there by
default.
More Examples
- The set of
positive integers.
- 1
is in POSINTS.
- If
x is in POSINTS then so is x+1.
- The set of
strings of x's of length > 0.
- x
is in L1.
- If
string w is in L1 then so is xw. (Prepend an x onto the string
w.)
- The set of
strings of x's of any length including 0.
 is
in L4.
is
in L4. - If
w is in L4 then xw is in L4.
- {xn
| n is odd}.
- x
is in L2.
- If
w is in L2 then xxw is in L2.
- The set of
decimal integers.
- 1,2,3,...,9
are in INTEGERS.
- If
w is in INTEGERS then so are w0, w1, w2, ..., w9.
- The closure of
a set of strings S.
 and
all the words of S are in S*.
and
all the words of S are in S*. - If
x and y are in S* then xy is in S*.
- Arithmetic
expressions using +, -, *, and /:
- Any
number is in the set AE.
- If
x is in the set AE then so are (x) and -x (if x doesn't already start
with -.) If x and y are in the set AE then so are x+y, x-y, x*y, and x/y.
We have used the
notation L* for the Kleene closure of language L. If L = {x} we could write
{x}* and mean the same thing. The braces don't really improve our understanding
so we will allow writing simply x* to mean the Kleene closure of the set {x}.
We will say that x* generates { ,
x, xx, xxx,� xxxx,� xxxxx ...}.
,
x, xx, xxx,� xxxx,� xxxxx ...}.
The * means 0 or more of. It applies
to the symbol or parenthesized expression to its left. The notation ab*
generates {a, ab, abb, abbb, abbbb, . . . .},
but (ab)* generates { ,
ab, abab, ababab, abababab, . . .}.
,
ab, abab, ababab, abababab, . . .}.
We use the superscripted + to mean 1
or more of. xx* = x+ and these generate {x, xx, xxx, xxxx, . . . .}.
ab*a generates {aa, aba, abba, abbba,
...}. a*b* generates { ,
a,b,aa,ab,bb,aaa,aab,abb,bbb,...}. This is the set of strings of 0 or more a's
and 0 or more b's where all the a's come before the b's.
,
a,b,aa,ab,bb,aaa,aab,abb,bbb,...}. This is the set of strings of 0 or more a's
and 0 or more b's where all the a's come before the b's.
x(xx)* = (xx)*x and these generate
strings of x's of odd length.
The plus symbol can also be used to
mean "or". In this case it is not superscripted. (x + y) means x or y
and this expression generates the set {x,y}. (a+c)b* = (a U c)b* which generates {a,c,ab,cb, abb,cbb,abbb, cbbb, ...}.
(a+b)(a+b) generates {aa, ab, ba, bb}. We could also generate this last
language with (a+b)2 but this is not usually done. (a+b)* generates
the closure of {a,b} = { ,
a,b,aa,ab,ba,bb,...}. This last expression is very useful and can be combined
with others as in a(a+b)* which generates words over {a,b} that start with a.
The expression a(a+b)*b generates words that start with a and end with b.
,
a,b,aa,ab,ba,bb,...}. This last expression is very useful and can be combined
with others as in a(a+b)* which generates words over {a,b} that start with a.
The expression a(a+b)*b generates words that start with a and end with b.
The expressions we have been using are
called regular expressions. The languages they define are called regular languages. For a detailed description of regular languages please visit this site
Here is a recursive definition of the set of regular expressions
over the alphabet Σ
1. Every element of alphabet (Σ) is a regular expression; ^ (null) is a regular expression.
2. If x and y are regular expressions, then so are x+y (union), xy (concatenation), x* (Kleene star), and (x).
3. Nothing else is a regular expression.
According to rule 2, union, concatenation, Kleene Star and parentheses can be used to create new regular expressions from old ones.
Suppose = { a, b }, then a and b are regular expressions according to rule 1. According to rule 2, ab, a+b, a* and (a) are also regular expressions
. Please note that a+b is often written as a U b (see Sipser, M. (2012) Introduction to the Theory of Computation , Course Technology.)
We use 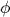 (phi)
to denote the regular expression that generates the empty language
(phi)
to denote the regular expression that generates the empty language 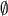 .
.
(a+b)*a(a+b)* generates strings
containing at least one a. The string aabab is such a string. How could we get
that string using the regular expression (a+b)*a(a+b)*? In three different
ways. The required a could be either the first, the second, or the third a in
aabab.
The expressions b* + (a+b)*a(a+b)* and
(a+b)* both generate the same language, the set of all strings over {a,b}. Why?
The only strings not generated by (a+b)*a(a+b)* are strings made completely of
b's. The expression b* + (a+b)*a(a+b)* generates the union of the two languages
1) strings made of 0 or more b's, and 2) strings containing at least one a.
This union contains all strings over {a,b}.
How would we write a regular
expression for strings that contain at least two a's? Note that it is not
necessary that the two a's be contiguous. One such regular expression is
(a+b)*a(a+b)*a(a+b)*. Another is b*ab*a(a+b)*. The difference in these two
regular expressions becomes obvious when you attempt to generate a particular
string using the regular expression. How would you generate babaaba? With the
first expression there are six different ways, but with the second expression
there is only one way. The required a's in the second expression must be the
first two a's of the string.
Two regular expressions are equivalent
if they generate the same set of strings. Here are some more regular
expressions for the language of strings containing at least two a's:
(a+b)*ab*ab* and b*a(a+b)*ab*. In the first one the required a's are the last
two a's of the string and in the second one the required a's are the first and
the last.
How would we write a regular
expression for strings containing exactly two a's? b*ab*ab*; it allows exactly two a's and zero or more b's
How about at least one a and at least
one b? Note that whatever regular expression we choose must be able to generate
both ab and ba. An expression that does the job:
- (a+b)*a(a+b)*b(a+b)*
+ (a+b)*b(a+b)*a(a+b)*
Here are some expressions that are
equivalent to (a+b)*:
- (a+b)*
+ (a+b)*
- (a+b)*(a+b)*
- (a*b*)*
- (a*+b*)*
- a(a+b)*
+ b(a+b)* +

- (a+b)*ab(a+b)*
+ b*a*
If a language is finite, a regular
expression for that language is just an OR of all the words in the language.
For example, if L = {ab, aba, bb} then a regular expression for L is ab + aba +
bb. If the language includes  ,
we add it to the regular expression as in
,
we add it to the regular expression as in  +
ab + aba + bb.
+
ab + aba + bb.
We can concatenate two languages in a
similar way to concatenating strings, except that we pair up and concatenate
all possible strings. If S = {a, aa, ba} and T = {bab, bb}, then ST contains
all strings that begin with an element of S and end with an element of T (with
nothing in between.) ST = {abab, abb, aabab, aabb, babab, babb} (not listed in
lexicographic order.) A regular expression for ST is (a + aa + ba)(bab + bb).
We define the language generated by
a regular expression this way:
- If
the regular expression is
 then
the language is {
then
the language is { }.
If the regular expression is a single symbol a from the alphabet,
the language is {a}.
}.
If the regular expression is a single symbol a from the alphabet,
the language is {a}.
- If
regular expression R1 generates language L1
and regular expression R2 generates language L2,
then (R1)(R2) generates L1 L2,
(R1)+(R2) generates L1
 L2 = L1+L2,
and (R1)* generates L1*.
L2 = L1+L2,
and (R1)* generates L1*.
Every regular expression generates
some language but not every language is generated by a regular expression.
Every finite language can be generated by a regular expression but many
infinite languages cannot.
Figuring out what language is generated
by a regular expression can be tricky. Try these:
- (a+b)*(aa+bb)(a+b)* strings
containing a double letter
- (
 +b)(ab)*
(
+b)(ab)*
( +a) strings
that do not contain any double letters
+a) strings
that do not contain any double letters
- b*(abb*)*(
 +a) strings that do not contain aa
+a) strings that do not contain aa
-
We draw a Finite Automaton (FA) below which accepts
any string from ab*.
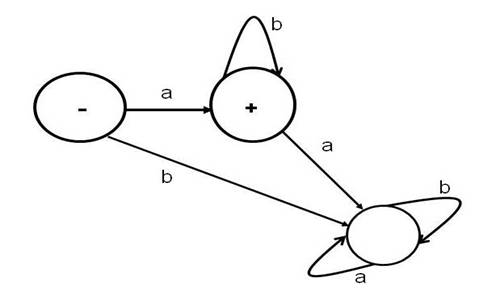
Please note that the Non-Deterministic
Finite Automaton (NFA) for the same regular expression, ab*, is
given below which looks simpler. Why? Because in order to meet the definition of FA there should be
one transition for every element of 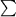 from each state, where as the NFA definition allows to have only a subset of them. .
from each state, where as the NFA definition allows to have only a subset of them. .
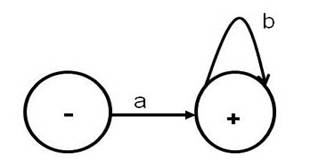
The above notation for FA and NFA is given in Daniel I. Cohen, 1997, Introduction to Computer Theory , 2nd Edition. Finite automata can be drawn with different notations. Please note that some books show the start state with an incoming arrow that is not attached to any other state (instead of a � sign). Accept states or final states are often drawn as double concentric circles in some books (instead of a + sign). Thus, the NFA for ab* would look as given below:
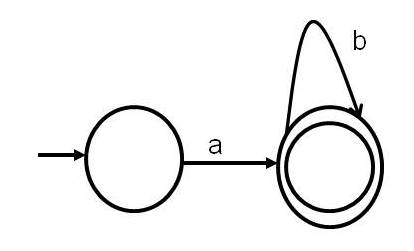
A Finite Automaton for (a+b)* or (a U b)* or (a|b)* is given below in Cohen's Notaion.

The same Finite Automaton for (a+b)* or (a U b)* or (a|b)* can be drawn as shown below:

(a+b)* = { ^, a, b, aa, ab, ba, bb, aaa, aba, aab, abb, baa, bba, bab, bbb, . . . }. That is, (a+b)* denotes a set that includes every string that can be made out of a & b. In other words, all possible combinations of a's and b's are in (a+b)* or (a|b)* or (a U b)*.
An NFA for a(a+b)* or a(a|b)* is given below in Cohen's Notaion.
We draw another finite automaton which accepts all
strings from a*bb*aa*(ba*bb*aa*)*.
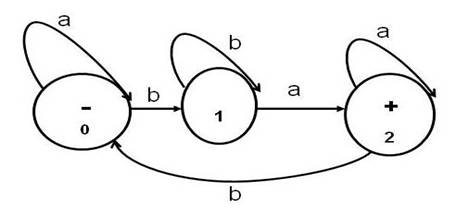
Please note that some books show the
start state with an incoming arrow that is not attached to any other state
(instead of a � sign). Accept states
or final states are often drawn as double concentric circles in some books (instead
of a + sign). States are given names
(0,1,2) to make discussions of the behavior of the
machine easier. Transitions are shown as labeled arcs from one state to another
or from a state back to itself. In the above, if the machine is in the start
state 0 and it reads an a, the transition leaves state
0 and reenters state 0. If it reads a b from state 0, the machine enters state
1.
It is common for each state to have a
transition leaving it for each letter of the alphabet. The above machine, when
given the string bbabba will end up in state 2 and
accept the string. If it reads string abbbab it ends
up in state 0 and does not accept the string. We say that the machine rejects abbbab.
Note that the author uses a slightly
different schema for drawing finite automata. He puts a minus sign in the start
state and plus signs in the accept states.
The set of strings accepted by a
finite automaton is referred to as the language accepted by the finite
automaton. We might describe a finite automaton as a language recognizer
whereas a regular expression is a language generator.
For each finite automaton there is a
regular expression that defines the same language. Later we will learn an
algorithm for determining the regular expression, but sometimes we can figure
it out using our common sense. Look back at the above finite automaton. A
regular expression corresponding to that machine is a*bb*aa*(ba*bb*aa*)*. Note that the portion before the parentheses moves
you from the start state to the accept state. The portion in the parentheses
moves from the accept state back to the accept state
and this expression is "starred" because you can repeat this cycle as
many times as necessary.
Another way to represent a finite
automaton is with a transition table. Here is the table for the above
machine. The rows correspond to states, the columns correspond to characters
from the alphabet, and the cell contents correspond to the transitions of the
machine.
|
State
|
a
|
b
|
|
0
|
0
|
1
|
|
1
|
2
|
1
|
|
2
|
2
|
0
|
A drawing of a finite automaton (FA) is
easier for a human to understand than a table, but implementing a machine with
a computer program requires storing the finite automaton's transitions in a
table. There is not just one FA, NFA or DFA for a given language; usually there are several alternatives. You may like to study Finite Automata and Regular Languages in details.
Useful Links for Automata
REFERENCES:
[1] Cohen, D. Introduction to Computer Theory. (2nd. Ed.). John Wiley, 1996.
[21 Hopcroft, J., Motwani, R., and Ullman, J. Introduction to Automate Theory, Languages, and Computation. (2nd. Ed) Pearson Education, 2007.
[3] Sipser, M. Introduction to the Theory of Computation, (3rd Ed.) Cengage Learning, 2012.
[4] Rodger, S, H,, . Bressler, B., Finley, T., and Reading, S. Turning automata theory into a hands-on course. In
Thirty-seventh SIGCSE Technical Symposium on
Computer Science Education, pp. 379-383. SIGCSE,
March 2006.















