Mathematical
Foundations
|
|
Finite Automata (FA) and Regular Expressions
(Based on
John E. Hopcroft, Rajeev Motwani, Jeffrey D. Ullman (2007). Introduction to Automata Theory, Languages, and Computation, 3rd Edition, Addison Wesley.,
M. Sipser (2012) Introduction to the Theory of Computation, 3rd Edition, Cengage Learning, and D. Cohen (1997) Introduction to Computer Theory, 2nd Edition, John Wiley & Sons )
|
|
Consider a wall switch that turns a light on and off. If the switch is up, the light is on. If it is down, the light is off. There are two possible states the switch can be in. The states are on and off.
We intend to build machines that have
states. We represent the states by
circles. The states may be connected by
transitions represented by arrows. Certain states are special. We call
such states final states. Instead
of the term final state, other equivalent terms such as terminal
state, and accept
state are also used.
A general model of such a machine is
called a finite automaton. The word finite refers to the fact that the
machine has a finite number of states. The terms Finite Automata(FA) and Deterministic Finite Automata (DFA) are used interchangeably.
A Finite Automaton (FA) is composed of
five components:
1. Q: A finite set of states.
2. 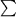 : A finite set of symbols, called the alphabet.
3. Q x
: A finite set of symbols, called the alphabet.
3. Q x 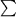 --> Q is the transition function.
4. q0 in Q is the start state, and
5. F is a set of final states (or accept states). F is a subset of Q.
--> Q is the transition function.
4. q0 in Q is the start state, and
5. F is a set of final states (or accept states). F is a subset of Q.
The component-3 of the above definition implies that there is one outgoing transition from ever state for every symbol of the alphabet (sigma). Please note that the alphabet does not include the ^ symbol (which stands for the null string). F can be empty; that is, there may not be any final state in an FA as indicated in component-5 of the above definition. For a simple example of an FA or DFA, please visit this website.
The input to a finite automaton is a
string of letters from the alphabet. The input is finite in length, that
is read left to right one character at a time. Beginning in the start state, the
machine reads a letter and makes a transition over and over until the string
ends. If this process ends with the machine in an accept state, we say that the
string is accepted. Otherwise the string is rejected.
For an animation of a finite automaton, please visit this website.
We draw a Finite Automaton (FA) in the
following manner: The machine’s states are represented by circles and
transitions are represented by arrows. Every transition is marked by a symbol from
the alphabet
The finite automaton given above has
one start state. Of course, every finite automaton has exactly one start state
by definition. The above finite
automaton has one final state although finite automata are allowed to have zero or more
final states. The set of strings accepted by a finite automaton is referred to
as the language accepted by the finite automaton (or the regular expression defined by the finite automaton). The above finite automaton accepts the language defined
by a*ba*. The
intuitive explanation is that the machine starts at the start state and can take the loop
transition marked by the symbol a from the start state zero or more times and
then take the arrow marked by b and reach the final state where it can take
the loop transition marked by a as many time as it likes and finish at
the final state marked in order to accept an input string. From the final state, if the transition marked by b is taken then the machine will reach
the non-final state that has two loops.
However, it
does not add to the language the machine accepts. Because, a finite automata’s accepted
language is defined by tracing the paths from the start state to the final
state(s). Paths ending in the non-final states do not contribute to the
accepted language of the machine. The above notation for finite automata is
given by M. Sipser (2012) Introduction to the Theory of Computation, 3rd Edition, Cengage Learning, and Hopcroft, Motwani & Ullman (2007) Introduction to Automata Theory, Languages, and Computation.
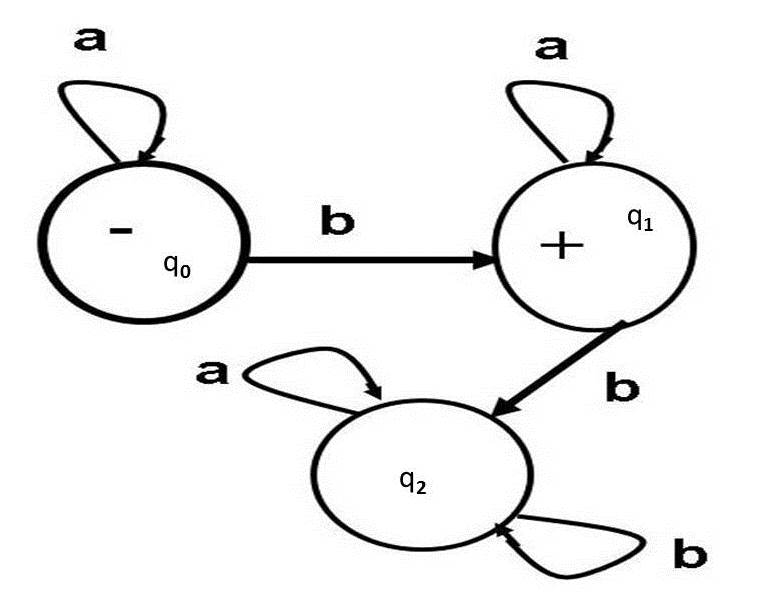
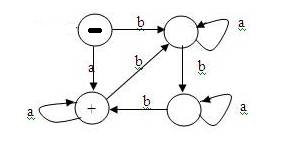
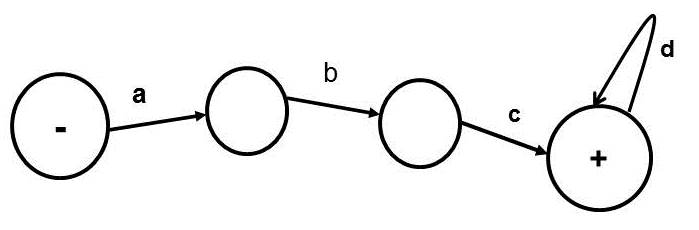
Finite automata can be drawn with different notations. The above FA for a*ba* is drawn below in Figure 2 in the notation of Cohen, 1997, Introduction to Computer Theory. In Cohen's notation the start state is marked by a - sign and the final states are marked by a + sign.
Figure 2: A Finite Automaton (FA) for a*ba* in Cohen's (1997) notation
Please note that the terms Finite Automata (FA) and Deterministic Finite Automata (DFA) are used interchangeably; by FA one means DFA. Non-Deterministic Finite Automata (NFA) are different from DFA, by definition; NFA are explained later.
We draw another Finite Automaton (FA) below which accepts
every string from ab*.
A type of dynamic visualization of the above FA is given at:
http://www.asethome.org/fa/. For a demonstration, please click here.
Please note that the Non-Deterministic
Finite Automaton (NFA) for the same regular expression, ab*, is
given below which looks simpler than FA or DFA.
Why? Because in order to meet the
definition of DFA or FA, there
should be one transition for every element of We draw another
FA or DFA which accepts all
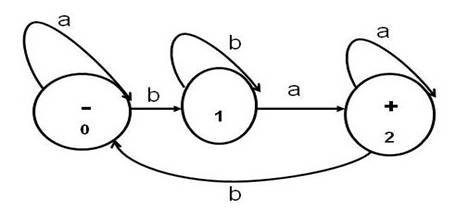
strings from a*bb*aa*(ba*bb*aa*)*. As mentioned before, please note that some books show the
start state with an incoming arrow that is not attached to any other state
(instead of a – sign). Accept states
or final states are often drawn as double concentric circles in some books
(instead of a + sign). States are given names
(0,1,2) to make discussions of the behavior of the
machine easier. Transitions are shown as labeled arcs from one state to another
or from a state back to itself. In the above, if the machine is in the start
state 0 and it reads an a, the transition leaves state
0 and reenters state 0. If it reads a b from state 0, the machine enters state
1. It is common for each state to have a
transition leaving it for each letter of the alphabet. The above machine, when
given the string bbabba will end up in state 2 and
accept the string. If it reads string abbbab it ends
up in state 0 and does not accept the string. We say that the machine rejects abbbab. Note that the author uses a slightly
different schema for drawing finite automata. He puts a minus sign in the start
state and plus signs in the accept states. The set of strings accepted by a
finite automaton is referred to as the language accepted by the finite
automaton. We might describe a finite automaton as a language recognizer
whereas a regular expression is a language generator. For each finite automaton there is a regular
expression that defines the same language. Later we will learn an algorithm for
determining the regular expression, but sometimes we can figure it out using
our common sense. Look back at the above finite automaton. A regular expression
corresponding to that machine is a*bb*aa*(ba*bb*aa*)*. Note that the
portion before the parentheses moves you from the start state to the accept
state. The portion in the parentheses moves from the accept
state back to the accept state and this expression is "starred"
because you can repeat this cycle as many times as necessary. Another way to represent a finite
automaton is with a transition table. Here is the table for the above
machine. The rows correspond to states, the columns correspond to characters
from the alphabet, and the cell contents correspond to the transitions of the
machine. State a b 0 0 1 1 2 1 2 2 0 A drawing of a finite automaton is
easier for a human to understand than a table, but implementing a machine with a
computer program requires storing the finite automaton's transitions in a
table. There is not just one finite
automaton for a given language. Typically it is possible to draw the finite
automaton in any of several different ways. There are languages for which it is
not possible to draw any finite automaton. For example, there is no FA for L3
= { anbn:
where n > 0 }. Later we will show that any language that can
be described by a regular expression can also be described by a finite
automaton and vice versa. A regular expression for the above
machine is (baa + abb)*. Can you find a regular
expression for this next one?
If you try running some strings
through the most recent machine you may notice that what it takes to get to the
accept state is to see either two a's in a row or two b's. So the regular
expression for the machine is (a+b)*(aa+bb)(a+b)*.
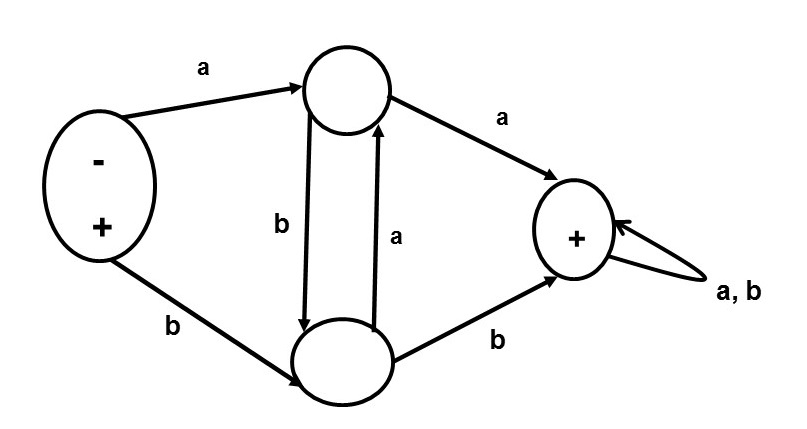
Let's try one more: Notice that this machine will accept
any string consisting entirely of a's. It will also accept any string in which
the number of b's is divisible by 3. Since the start state is not an accept
state, the machine does not accept How do you create a finite automaton
that will accept any string with an odd number of a's? As the machine reads
a's, you need to move back and forth between two states, one where the number
of a's so far is even and one where the number is odd. Since we are not
concerned with the number of b's, each state should have a self-transition for
a b (a transition that leaves and enters the same state.) Which of the two
states should be the start state? Since 0 is even and at the beginning we have
seen 0 a's, the start state should be the state that corresponds to having seen
an even number of a's. The other state, the one for having seen an odd number
of a's, is an accept state. A machine that accepts strings with an even number
of a's would look just like the one for odd a's except that the other state is
the accept state. What if we are concerned about the
parity (oddness or evenness) of both a's and b's? For example, we might want to
accept strings that contain an odd number of a's and an even number
of b's. To figure out how many states we need we must ask how many different
combinations of odd and even there are for two letters. The answer to this
question is four: even/even, even/odd, odd/even, and odd/odd. The even/even
state is the start state. Which states are accept
states depends on the language we wish to accept. If we want strings that
contain an odd number of a's and an even number of b's
then we make the state odd/even be the only accept state. If we want strings in
which the parity of a's matches the parity of b's then we make both even/even
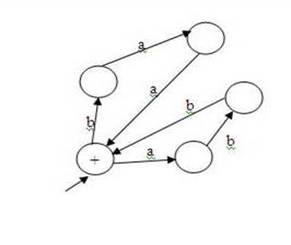
and odd/odd be accept states. Here is one final example of a finite
automaton. What strings are accepted by this one? There are two accept states in this
machine. In order to get to the top one, the first letter of the string must be
a and the last letter must be b. In order to get to
the bottom one, the first letter must be b and the last one a. So this machine
accepts strings that start and end with a different letter. There is no way to
do this job with a single accept state. The machine must remember what the
first letter was by taking one or the other of the transitions off of the start
state. Once the machine has taken either the "high road" or the "low
road" it cannot leave that portion of the machine or it would
"forget" the first letter. The following
Non-deterministic Finite Automaton would accept
any string from the regular expression
b*aba*b.
A nondeterministic finite automaton (NFA) is composed of 5 components:
It is to be noted that the component-3 of the above definition implies
that null-transitions (that is, transitions with the null symbol, ^,) are also allowed in NFA.
It is proven by Kleene that NFA are
equivalent to Deterministic FA. A
DFA (Deterministic FA )for b*aba*b is given below:
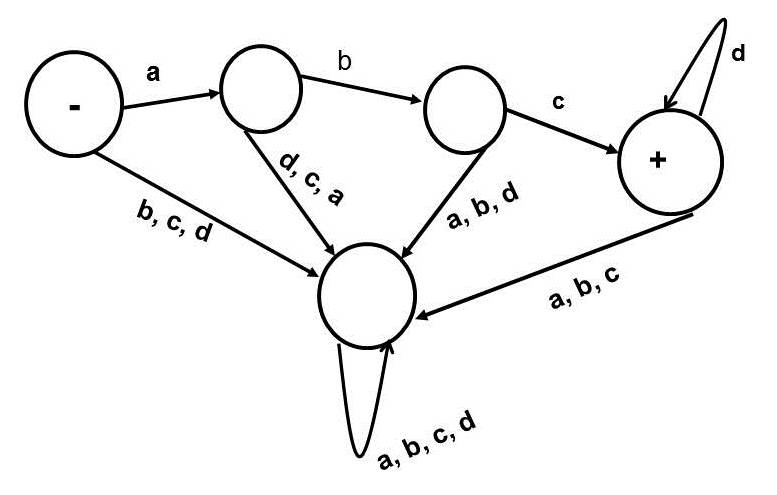
Consider the following NFA (Non-deterministic Finite Automaton) for abcd*.
A DFA (Deterministic Finite Automaton) for the same regular expression (abcd*) is given below:
R1R2, R1+R2, R1* and
(R1).
Accourding to rule 2, concatenation, union, Kleene Star and parentheses can be used to create new regular expressions from old ones.
Suppose
Consider the following example:
The regular expression, 1*, includes an infinite set of strings given in
{^, 1, 11, 111, 1111, 11111, . . . }. From the same alphabet consider the following two regular expressions:
11* = {1, 11, 111, 1111, 11111, . . . }
11*1 = {11, 111, 1111, 11111, 111111, . . . }
Consider another example of regular expression given below:
Please note that the alphabet (sigma) is often not mentioned, if it is understood in the context. Thus, the following regular expression implies that the alphabet is {a, b}.
abba* = {abb, abba, abbaa, abbaaa, abbaaaa, . . . }
Please click here to go back to the Mathematical Foundations home page .
Chapter
6 - Transition Graphs (See Cohen (1997) Introduction to Computer Theory, 2nd Edition, John Wiley & Sons, for details )
In this chapter we
define a new type of finite state machine called a transition graph.
These machines were invented in 1957 by John Myhill
in order to simplify the proof of a theorem known as Kleene's
Theorem. A Transition Graph (TG) is basically a generalized nondeterministic
finite automaton.
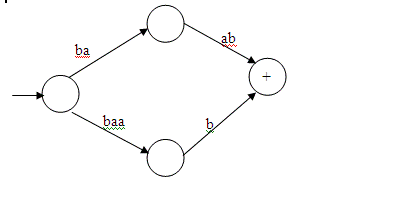
The following features of TG’s are emphasized: Here is an example
of a transition graph that illustrates some of the quirks of such machines. In
this machine there are two different accepting paths that the machine may take
on the string baab. There is no path at all for
strings other than baab, so the string abb is rejected as are all strings other than baab. If any path for a particular input
leads to an accept state, we say the string is accepted. What if one path for
string X leads to an accept state and one to a non-accept state? Then that
string is accepted. Self-Checking
Exercises: (You
are encouraged to do these exercises. You are not required to submit them)
For suggestions on studies of related application areas, please visit this website. ![]() . The start state is marked by a special short arrow that comes from nowhere, and the final states are marked by double circles. (For an explanation of
a*ba*, please click here.)
. The start state is marked by a special short arrow that comes from nowhere, and the final states are marked by double circles. (For an explanation of
a*ba*, please click here.)

Figure 1: A Finite Automaton (FA) for a*ba*

![]() from each state, whereas this restriction does not apply to NFA. .
from each state, whereas this restriction does not apply to NFA. . 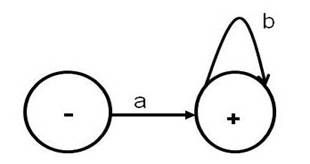
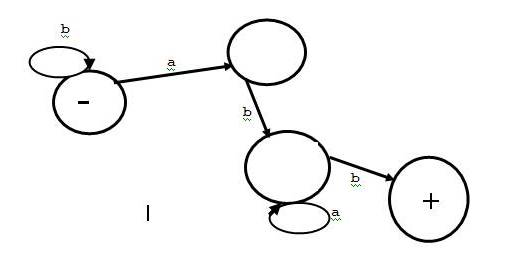
![]() .
A regular expression for the machine is (aa* + ba*ba*ba*)(a + ba*ba*ba*)*.
.
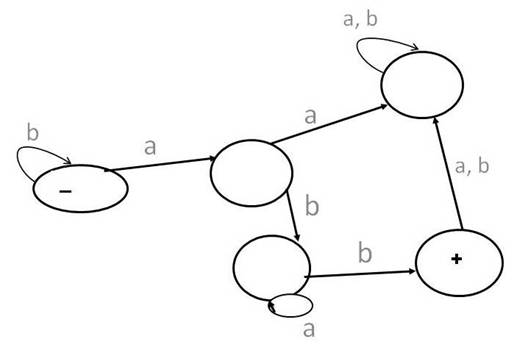
A regular expression for the machine is (aa* + ba*ba*ba*)(a + ba*ba*ba*)*. 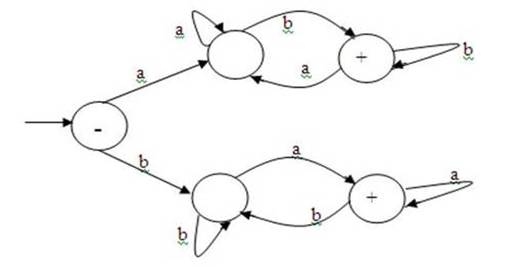
Non-deterministic Finite Automata (NFA) are distinct from the
Deterministic FA or DFA (or FA) because NFA do not require one
outgoing transition from every state for each symbol of the alphabet.
(see Sipser (2005) page 48).
1. Q: A finite set of states.
2.
![]() : A finite set of symbols, called the alphabet.
3. Q x
: A finite set of symbols, called the alphabet.
3. Q x ![]() U ^ --> Powerset(Q) is the transition function.
4. q0 in Q is the start state, and
5. F is a set of final states (or accept states). F is a subset of Q.
U ^ --> Powerset(Q) is the transition function.
4. q0 in Q is the start state, and
5. F is a set of final states (or accept states). F is a subset of Q.
![]() :
:
![]() is a regular expression. ^ is a regular expression.
is a regular expression. ^ is a regular expression.
![]() = { a, b }, then a and b are regular expressions according to rule 1. According to rule 2, ab, a+b, a* and (a) are also regular expressions
. Please note that a+b is often written as a U b (see Sipser, M. (2006) Introduction to the Theory of Computation , Course Technology.)
= { a, b }, then a and b are regular expressions according to rule 1. According to rule 2, ab, a+b, a* and (a) are also regular expressions
. Please note that a+b is often written as a U b (see Sipser, M. (2006) Introduction to the Theory of Computation , Course Technology.)
![]() = {1 }
= {1 }
1* = {^, 1, 11, 111, 1111, 11111, . . . }
![]() = {0, 1}
= {0, 1}
01* = {0, 01, 011, 0111, 01111, 011111, . . . }
![]() as a transition label. This is
interpreted as a "free move" from one state to another, a move
that does not involve reading any input.
as a transition label. This is
interpreted as a "free move" from one state to another, a move
that does not involve reading any input.