If aabbaa is entered, then it would be accepted by the above machine. If aabba is entered, then the machine
would NOT accept it, because the pattern anbnan (equal number of a's, followed by equal number of b's, followed by
equal number of a's) would be violated.
Logically speaking, the class of Turing Machines is the most powerful class of computing machines. Any problem
that can be solved computationally can be solved by a Turing Machine. Thus, computability means Turing computability.
In order to get a basic understanding of a Turing Machine, let us start with a “state machine” that simulates an on-off
switch of an ordinary light. This state machine has only two states, named on and off represented by two circles
which are connected by two transitions. The transitions are given by arrows which are labeled by turn-on and turn-off respectively.
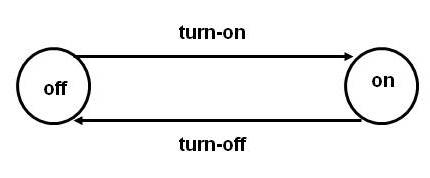
Figure 1. A state machine for modeling an on-off switch
According to the state machine of Figure 1, the switch is either in the off state or in the on state. Assume that the machine is initially in the off state. It is turned on by taking the transition (arrow) labeled turn-on after which it is in the on state. From the on state the transition labeled turn-off can be taken in order to reach the off state. Like the above state machine a Turing Machine has states represented by circles and transitions represented by arrows; however unlike the above state machine, a Turing Machine can have some special HALT states which cannot have any out going transition; that is, the HALT states can only have incoming transitions. For a description of Turing Machines a text book such as "Introduction to Computer Theory, 2nd Edition, by Daniel I. Cohen, published by John Wiley & Sons can be consulted.
For some preliminary interactions with Turing Machines, visualization of some additional machines can be found at the end of this section. After you follow the link given below, you will be asked to select one of the following two options:
(1) ab*
If you select this option, then you may type a string such as abbbb
in the white editable input field and then click on the
Process button. This Turing Machine accepts any string with one a
followed by any number of b's
(2) anbncn
If you select this option, then you may type a string such as aabbcc
in the white editable input field and then click on the
Process button. This machine accepts any string with equal number of a's
b's and c's
You can pause the machines and then run them again. You can enter any string made out of
a's and b's for experimental purposes. Please click on the link given below for the additional Turing Machines.
A Sample Demo on interactions with Turing Machines.
For questions and comments, please contact:
Dr. Pradip Peter Dey,
Professor, School of Engineering, Technology and Media
National University
3678 Aero Court, San Diego, CA 92123
U.S.A.
Phone: (858) 309-3421
Fax (858) 309-3420
Email: pdey@nu.edu
For more on Turing Machines, please click here.
You are requested to fill out every field; however, a partially filled out form is also accepted. That is, every field is optional.