Finite Automata (FA) accept regular languages such as ab* . However, FA do not accept non-regular Context-Free Languages such as Lm = { {nc}n : where n >= 0 }. It is to be noted that Lm has strings with a matching number of {'s and }'s separated by a c . What is interesting about L m is that it has a string pattern that is similar (but not exactly the same) to that of programming languages such as Java and C++. In fact, syntactic structures of a programming language are defined by Context-Free Grammars in a way that is similar to that of the Context-Free Grammar (CFG) of L m given below:
S -> {S} | c
This CFG generates or derives a balanced number of {'s and }'s. Pushdown Automata
are designed to accept languages with strings that have similar patterns. That is, a Pushdown
Automaton will accept strings like {c},
{{c}}, {{{c}}}, . . . ., (that is, the strings of Lm). Pushdown Automata
use a stack data structure for matching equal number of
{'s and }'s without counting them directly.
A stack is an interesting data-structure which allows operations such as
push and pop and increase or decrease its stored contents in a
Last-In-First-Out (LIFO) manner. Stacks are used for processing
Context-Free Languages.
Pushdown Automata are described in text-books such as [1] Hopcroft, J., Motwani, R.,
and Ullman, J. Introduction to Automata Theory, Languages, and Computation, Pearson Education, 2007.
[2] Cohen, D., Introduction to
Computer Theory, 2nd Edition, New York, NY: John Wiley & Sons, 1997. [3]
Lewis, H. R. and Papadimitriou, C. H., Elements of the Theory of Computation,
2nd Edition, New Jersey: Prentice_Hall, 1998.
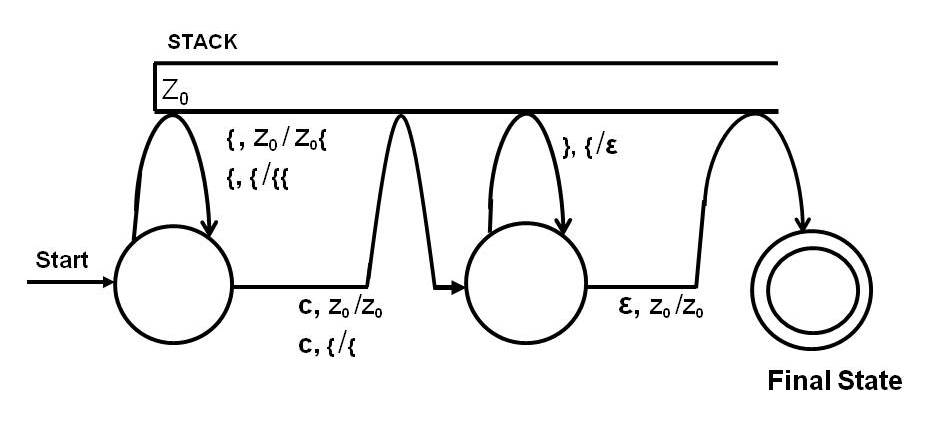
Pushdown Automata can be presented in various ways. In the following example, a Pushdown Automaton is presented visually as a finite set of states connected with transitions which is based on the notations of Hopcroft et al 2007 [1] with some minor adjustments.
Example 1: A Pushdown Automaton for Lm = {
{nc}n : where n >= 0 }. 
Suppose a string like {{c}} is given as an input to the above Pushdown Automaton (PDA). The machine starts at the start state and scans the first { from the input and pushes a { into the stack by taking the transition marked by, { , Z0 / Z0{ . The meaning of this transition label is "when reading a { and the stack is empty (marked by Z0) push a { onto the empty stack (marked by Z0)". Then it consumes the next { from the input by taking the same loop with the transition marked by {, { /{{ . Next, it consumes the symbol c by taking the transition marked by c, { /{ which means "read a c from the input when there is a { on top of the stack and leave the stack unchanged". Next, it reads the fourth symbol, } , from the input and pops a } from the stack taking the transistion marked by }, { /e . Then, it scans the next } by taking the same transition marked by }, { /e again. Then, it reaches the final state by taking the transition marked e, Z0 /Z0 . At that moment stack is empty and the entire input is consumed and therefore the input {{c}} is accepted by the machine. The PDA given above accepts any string with a sequence of {'s followed by a c followed a number of }'s that balances {'s. That is, strings such as c, {c}, {{c}}, {{{c}}}, . . . . are accepted by the machine. An input is accepted by a PDA if all of the following conditions are met simultaneously:
(1) the input is entirely consumed, that is, no other symbols left in the input;
(2) the machine is in a final state;
(3) the stack is empty.
According to Hopcroft et al 2007 [1], a Pushdown Automation (PDA), P, �is composed of the following seven components
���
P� =� (Q,�
∑, Γ,� δ, q0,
Z0, F)
�The components have the following meanings:
Q:�� A finite set of states, like the states of a finite automaton.
∑: ��A finite set of input symbols, also analogous to the corresponding component of a
finite automaton.
Γ:��
A finite stack alphabet.� This component, which has no finite-automaton� analog, is
the set of symbols that we are allowed to push onto the stack.
�δ:� The transition
function.� As for a finite automaton,
δ governs the behavior of the
automaton. Formally, δ takes as
argument a triplet� δ(q,
a, X), where :
1.
�q� is a
state in� Q
2.
a� is either an input symbol in� ∑�
or� a = ε,� the empty string, which is assumed not to be
an input symbol.
3.
��X is a stack symbol, that is,� a member of��� Γ.
The output of� δ is a finite
set of pairs (p, γ), where p is the new state,� and��
γ is the string of stack symbols that
replaces� X at the top of the stack. For
instance,� if� γ = ε, then the stack is
popped,� if�� γ = X, then the stack is
unchanged,� and if� γ = YZ, then� X is replaced by Z,� and Y is pushed onto the stack.�
q0:�
The start state.� The PDA is in
this state before making any transitions.
Z0 :� The start
symbol.� Initially,� the PDA�s stack consists of one
instance of this symbol, and nothing else.
F:� The set of accepting states,� or final
states. � �Hopcroft
et al 2007 [1]�
�
Pushdown Automata are interesting for their processing power of non-regulare Context-Free Languages such as Lm which are similar to programming languages.
For an animation of PDA, please visit this site .
Formal definitions of PDA can be found in [1,2, 3]. The following definition of PDA is basically taken from Cohen (1997).
Definition of Pushdown Automata
A pushdown automaton (PDA) is a
collection of eight things:
� An alphabet ∑ of input letters.
� An input
TAPE (infinite in one direction), which initially contains the input string to
be processed followed by an infinite number of blanks, ∆
� An alphabet E of
STACK characters.
� A pushdown STACK (infinite in one direction), which
initially contains all blanks, ∆.
� One START state that has only out-edges,
no in-edges. Can have more than one arc leaving the START state. There are no
labels on arcs leaving the START state.
� Halt states of two kinds:
1.
zero or more ACCEPT states
2. zero or more REJECT states
Each of the
Halt states have in-edges but no out-edges.
Finitely many nonbranching
PUSH states that introduce characters from E onto the top of the STACK.
Finitely many branching states of two kinds:
1. READ states, which read the
next unused letter from TAPE and may have out-edges labeled with letters from ∑
or a blank, ∆. (There is no restriction on duplication of labels and no
requirement that there be a label for each letter of ∑, or ∆.)
2. POP
states, which read the top character of STACK and may have out-edges labeled
with letters of E and the blank character ∆, with no restrictions.
A pushdown automaton for { anbn : where n >= 0 } is
given below which is taken from Cohen (1997) 
References:
[1] Hopcroft, J., Motwani, R., and Ullman, J. Introduction to
Automata Theory, Languages, and Computation, Pearson Education, 2007
[2] Cohen, D., Introduction to Computer Theory, 2nd Edition,
New York, NY: John Wiley & Sons, 1997.
[3] Lewis, H. R., and
Papadimitriou, C. H., Elements of the Theory of Computation, 2nd Edition, New
Jersey: Prentice_Hall, 1998.
[4] W. A. Woods, Transition network grammars
for natural language analysis, Communications of the ACM, v.13 n.10, p.591-606,
Oct. 1970
[5]
Sipser, M., Introduction to the Theory of Computation, 2nd Edition, PWS
Publishing, 2006.
[6] Goddard, W. (2009) Introducing the Theory of Computation, Jones & Bartlett Publishers.
[7] Kozen, D. (2006). Theory of Computation. Springer .
[8] Rich, E. ( 2007) Automata, Computability and Complexity: Theory and Applications